说明：催化”（Active Site）。从宏观上看，活性位点是催化剂表面或内部那些能够与反应物分子发生特定相互作用，显著降低反应能垒，从而加速化学反应速率的微观区域。

。在原子尺度上精确地识别、表征并最终理性设计高效的活性位点，是催化科学领域长期追求的圣杯。

本文将系统阐述理论计算，特别是及其衍生方法，如何从静态电子结构、反应路径能量学以及动态演化等多个维度，对催化活性位点DOI: 10.1021/acscatal.8b01924

活性位点的静态表征：电子结构是关键

。理论计算的首要任务便是精确描述这些位点的静态几何结构与电子结构。密度泛函理论（）在此方面扮演了核心角色。

在实际计算中，通常采用如维也纳从头算模拟软件包（VASP）等成熟的商业或开源软件，结合平面波基组和投影增广波（PAW）方法，来实现对复杂催化体系的高效模拟。

的选择，如广义梯度近似（GGA），是决定计算精度的关键所在。通过结构优化计算，研究者可以得到活性位点在原子尺度的精确几何构型，包括键长、键角以及与载体的配位方式等关键信息，这是理解其催化行为的第一步。

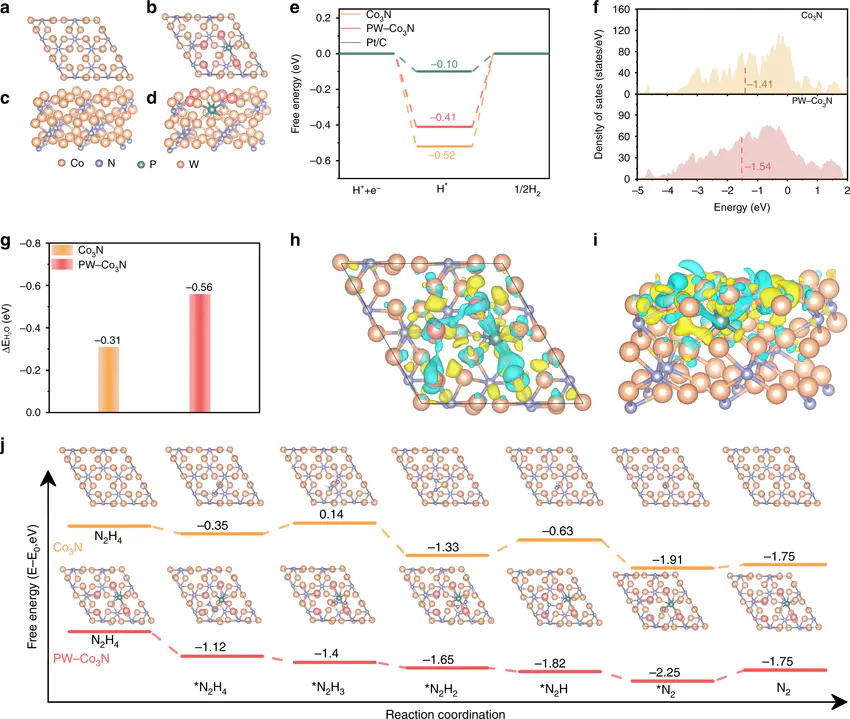
然而，几何结构只是冰山一角，活性位点的“活性”根源于其独特的电子结构。理论计算为我们提供了多种强大的分析工具来量化这些电子性质。

是一个极具影响力的理论框架。该模型指出，过渡金属表面的d电子能带中心的能量位置，与反应物分子在其上的吸附强度密切相关。一个d带中心更靠近费米能级的金属，通常会与吸附物形成更强的化学键这种相互作用强度遵循一个“火山型”关系：吸附太弱，反应物无法有效活化；吸附太强，产物又难以脱附，导致活性位点中毒。

（DOS），确定其d带中心的位置，就可以有效预测其催化活性趋势，例如在电催化氧还原反应（ORR）中，d带中心理论成功地解释了不同过渡金属的活性序列。

除了d带中心，通过Bader电荷DOI：的真正威力在于其与先进谱学实验的紧密结合。实验可以直接测量催化剂的宏观或平均性质，但往往难以给出原子级别的精确结构信息，而理论计算恰好可以弥补这一不足。

一个强大的联用策略是，将射线吸收光谱（XAS），特别是扩展X射线吸收精细结构（EXAFS）和高能分辨率荧光检测X射线近边吸收谱（HERFD-XANES）相结合。

构建一个包含各种可能构型（如不同的配位数、配位原子类型、几何畸变等）的结构库。随后，对库中的每一种结构进行理论XAS谱图的模拟，并与实验测得的谱图进行比对拟合。

例如，在一项结合了DFT-TDDFT计算和原位光谱的研究中，成功揭示了氮缺陷石墨相碳氮化物（g-C3N4）中，氮空位（Nv）才是光催化氧化反应理论计算表明，该氮空位能够有效吸附并活化O₂分子，同时抑制光生电子–空穴的复合，从而完美解释了实验观察到的催化性能提升。这种理论与实验的“握手”，使得我们能够从纷繁复杂的实验信号中，精准地“看到”活性位点的真实面貌。

可视化催化过程：反应路径与能量图

这通常通过计算反应自由能图Reaction Coordinate在这张图上，我们可以清晰地识别出反应物（Reactants）、中间体（Intermediates）、过渡态（Transition States, TS）和产物（Products）的能量位置。

是能量最高的点，其与反应物之间的能量差即为反应的活化能垒（Activation Barrier）。根据过渡态理论，活化能垒越低，反应速率越快。

为了更形象地说明这一过程，我们可以想象一张研究在不同活性位点上进行分解反应的理论计算图谱。这张图的横坐标是NO分子在催化剂表面的解离过程，纵坐标是能量。

。例如，一条蓝色曲线所代表的“A位点”，其从NO吸附态到N和O原子分离的过渡态，需要跨越一个非常高的能量山峰，这表明其活化能垒很大，催化活性很低。

更进一步，通过分析B位点的几何和电子结构此外，流程图也可以清晰地展示如何基于DFT计算的位点能量，结合机器学习模型，实现对催化剂活性的高通量筛选和优化设计，从而加速新材料的发现进程。

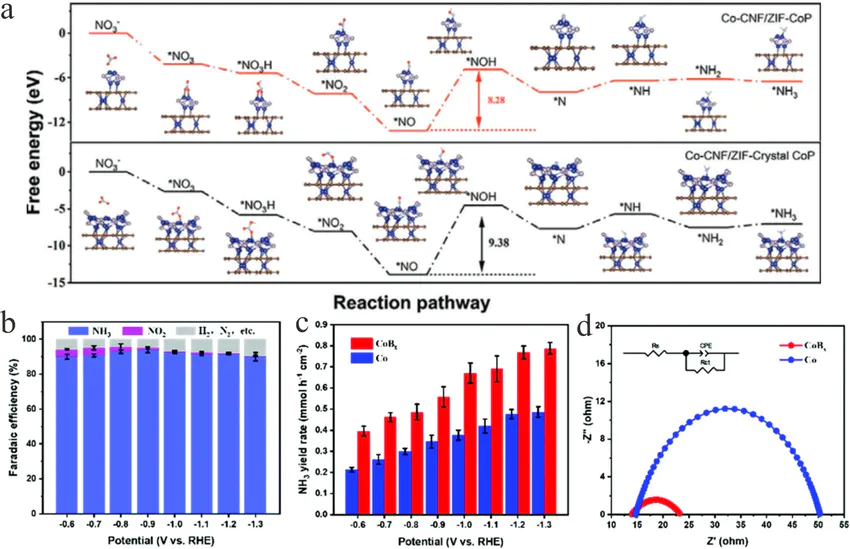
这些能量图谱不仅是数字的堆砌，更是对化学反应内在规律的可视化呈现。例如，在前面提到的氮缺陷碳氮化物催化体系中，理论计算可以生成电荷密度差分图我们可以清晰地“看到”，电子云密度从氮空位周围富集的区域，转移到了吸附的O₂分子的反键轨道上。

传统的催化模型往往将活性位点视为一个刚性的、静态的实体。然而，越来越多的证据表明，催化剂“operando”活性位点的几何构型、配位环境甚至电子态都可能随着温度、压力和反应物浓度的变化而发生重构。这种动态行为对催化性能有着至关重要的影响，而仅仅依赖于0K下的静态DFT计算是无法捕捉到的。

结合了量子力学的精确性和分子动力学的时间演化能力，它在每一个时间步长都通过DFT计算原子间的相互作用力，然后根据牛顿运动定律来更新原子核的位置和速度，从而模拟出体系在有限温度下的动态轨迹。

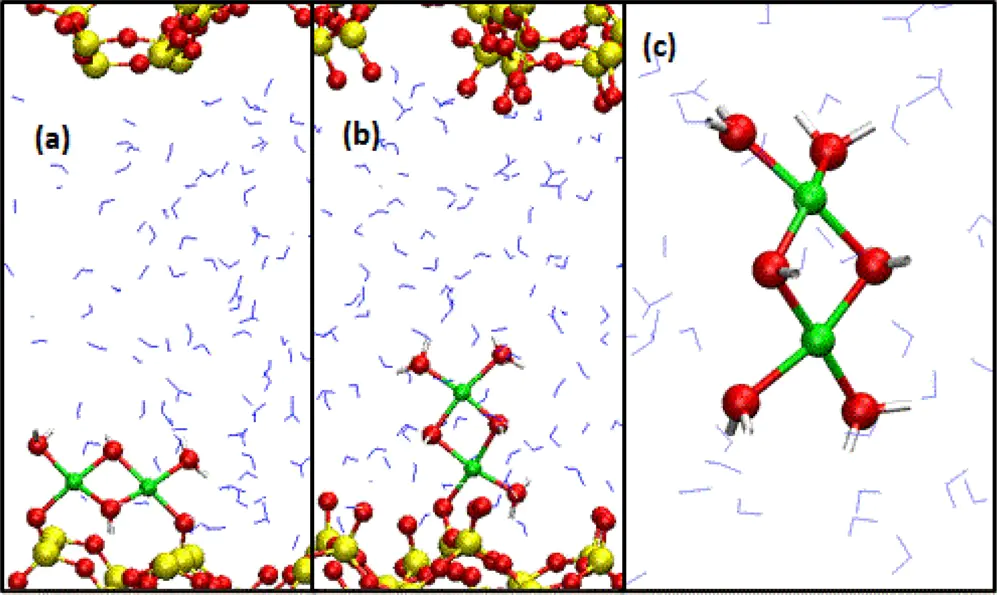
10.1038/s42004-022-00688-2

AIMD，我们可以研究催化剂表面的原子如何振动、扩散和重组，以及活性位点与溶剂分子、反应物分子之间的动态相互作用。

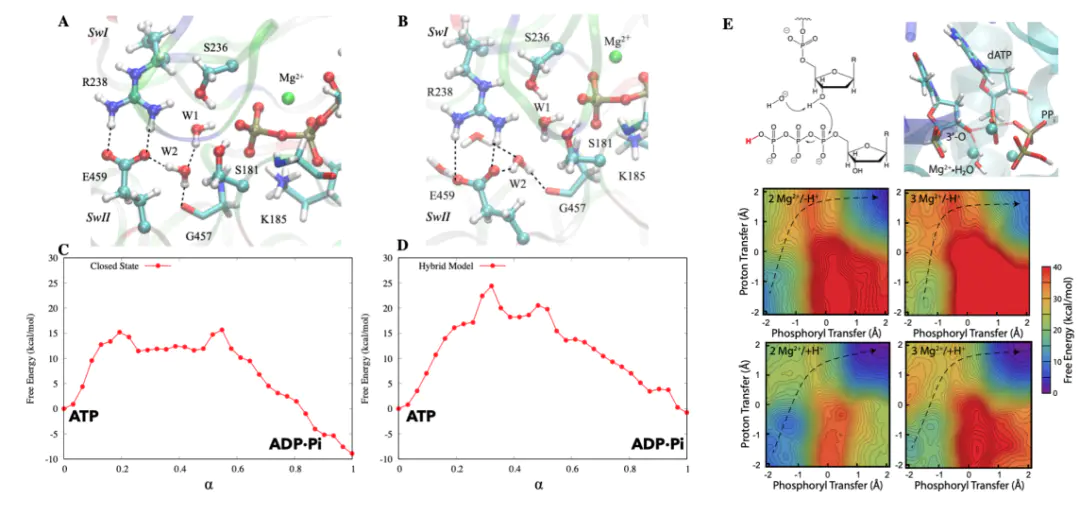
一个更为精妙的例子来自于生物催化领域，即对酶活性位点的研究。一项结合了分子动力学和量子力学分子力学（QM/MM）计算的研究，探讨了cAMP依赖性蛋白激酶（PKA）中激活环的磷酸化对其催化活性的影响。

这种动态的、非共价的相互作用，极大地稳定了高能量的过渡态，从而显著降低了反应能垒这个案例完美地诠释了，活性位点的功能不仅取决于其静态结构，更取决于它在反应过程中的动态行为和与环境的协同作用。

结论与展望

d带中心、电荷态）以及在反应条件下的动态行为共同定义的功能中心以密度泛函理论随着计算方法的不断进步和计算能力的持续增长，理论计算在催化研究中的作用将更加举足轻重。将与增强采样方法、机器学习力场理论计算与原位/工况表征技术的融合将更加紧密，形成一个从理论预测到实验验证再到理论修正的闭环研究范式。