[LG]《Why Can't Transformers Learn Multiplication? Reverse-Engineering Reveals Long-Range Dependency Pitfalls》X Bai, I Pres, Y Deng, C Tan... [University of Chicago & MIT & University of Waterloo] (2025)
多位数乘法,为什么大规模Transformer模型屡屡失败?
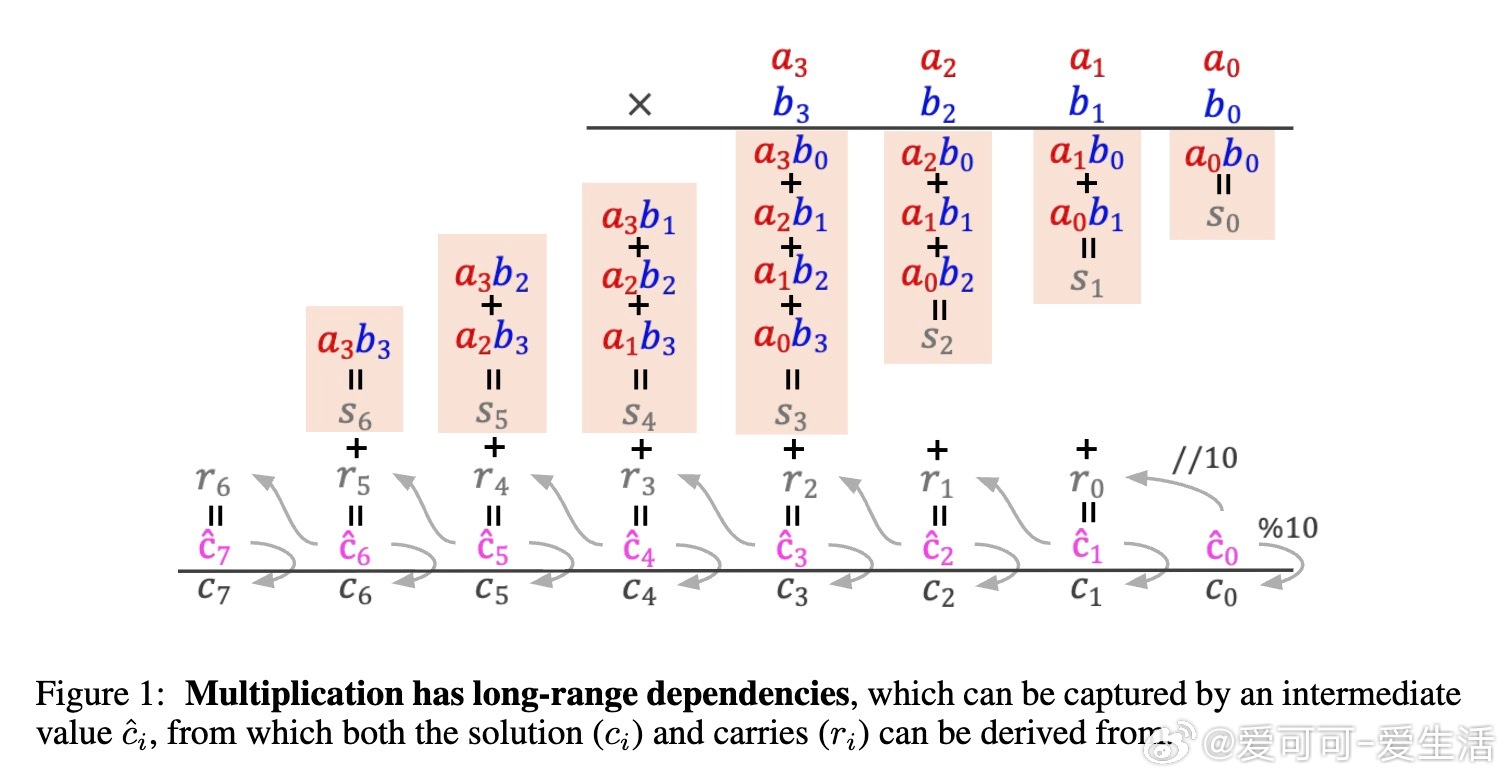
• 乘法本质依赖长距离信息传递:每位结果数字 \( c_k \) 需要聚合所有部分乘积 \( a_i b_j \) 满足 \( i + j \leq k \),以及前一位的进位信息,体现了极强的长程依赖。
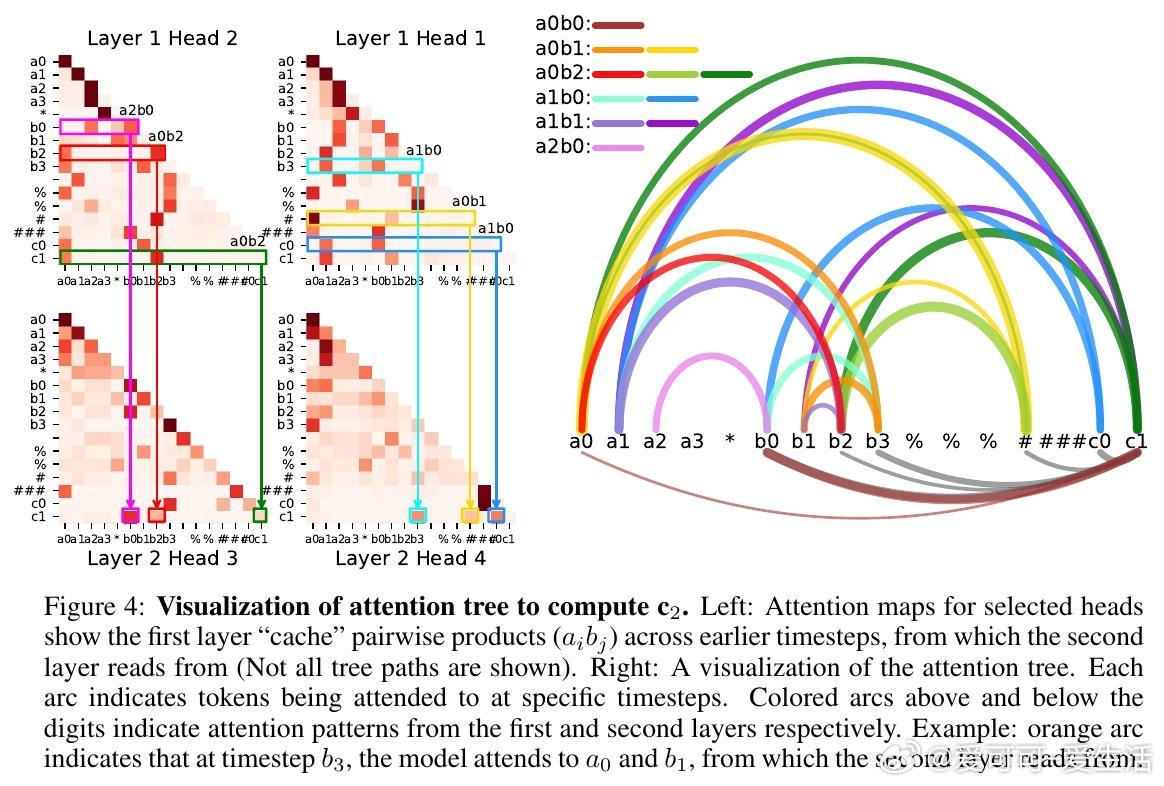
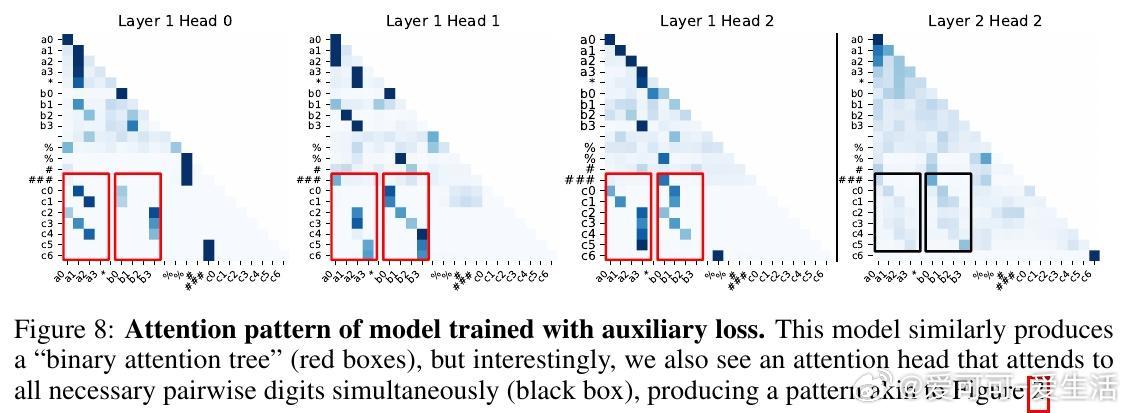
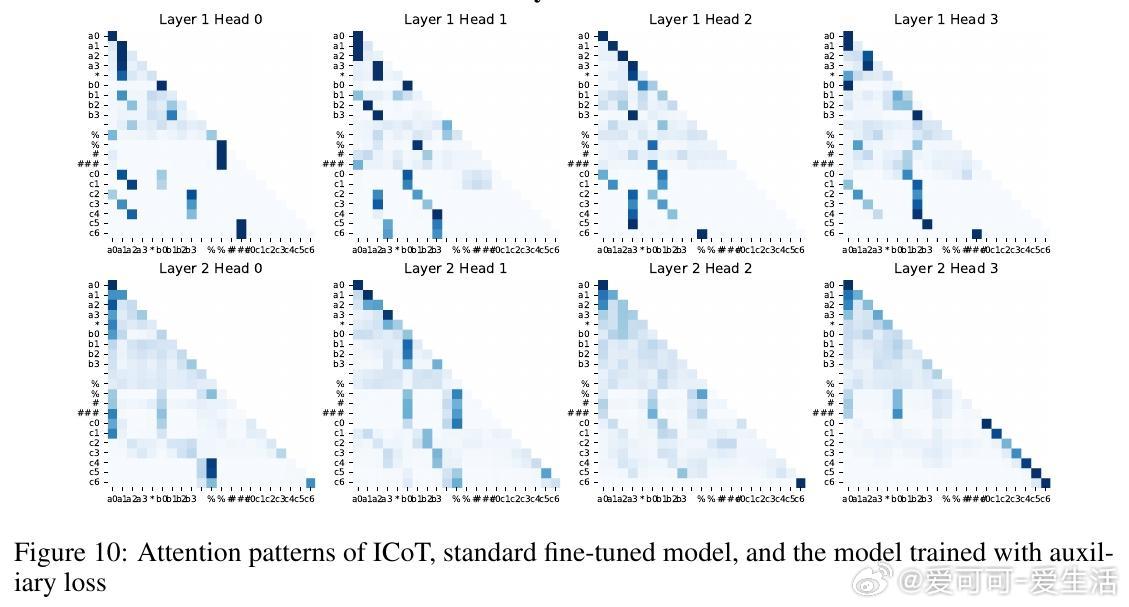
• ICoT(隐式链式思维)训练策略成功破解难题:通过训练初期引入显式链式思考步骤,逐渐移除辅助推理标记,模型学会内部“缓存-检索”机制,将乘积部分分解成有向无环图结构,形成“注意力树”捕获关键数字对乘积。
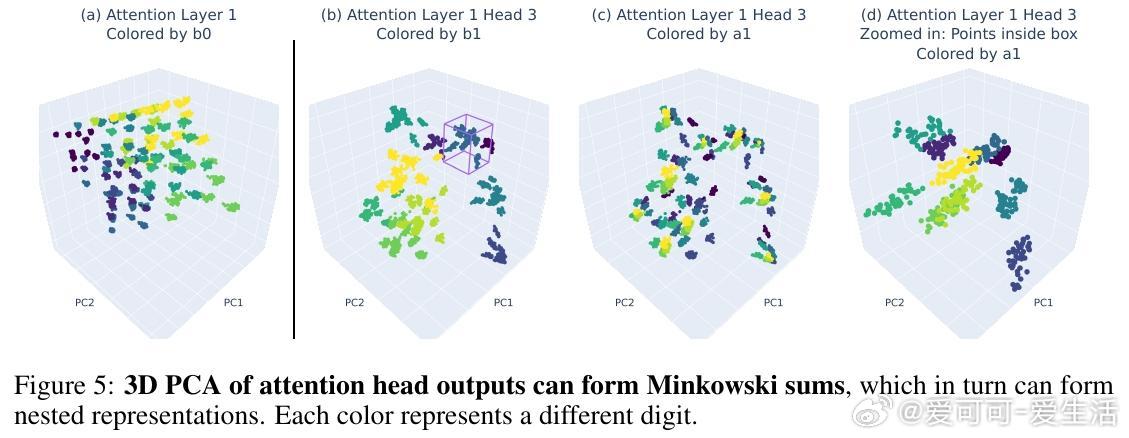
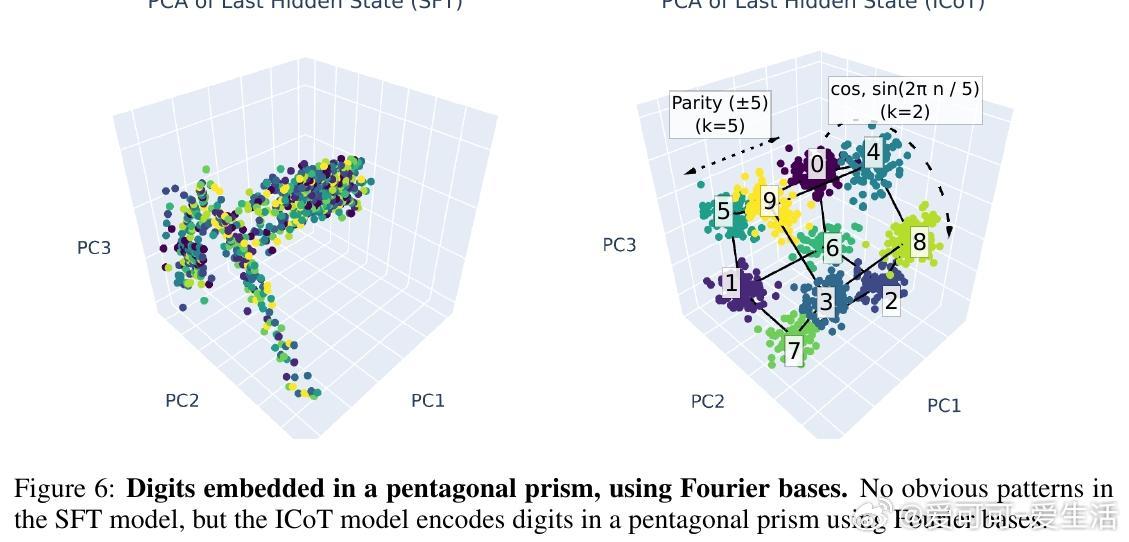
• 几何表征创新:ICoT模型将数字嵌入傅里叶基底,部分乘积对应注意力头输出的Minkowski和,数字在特征空间呈现五边形棱柱结构,极大提升了表示效率与推理精度。
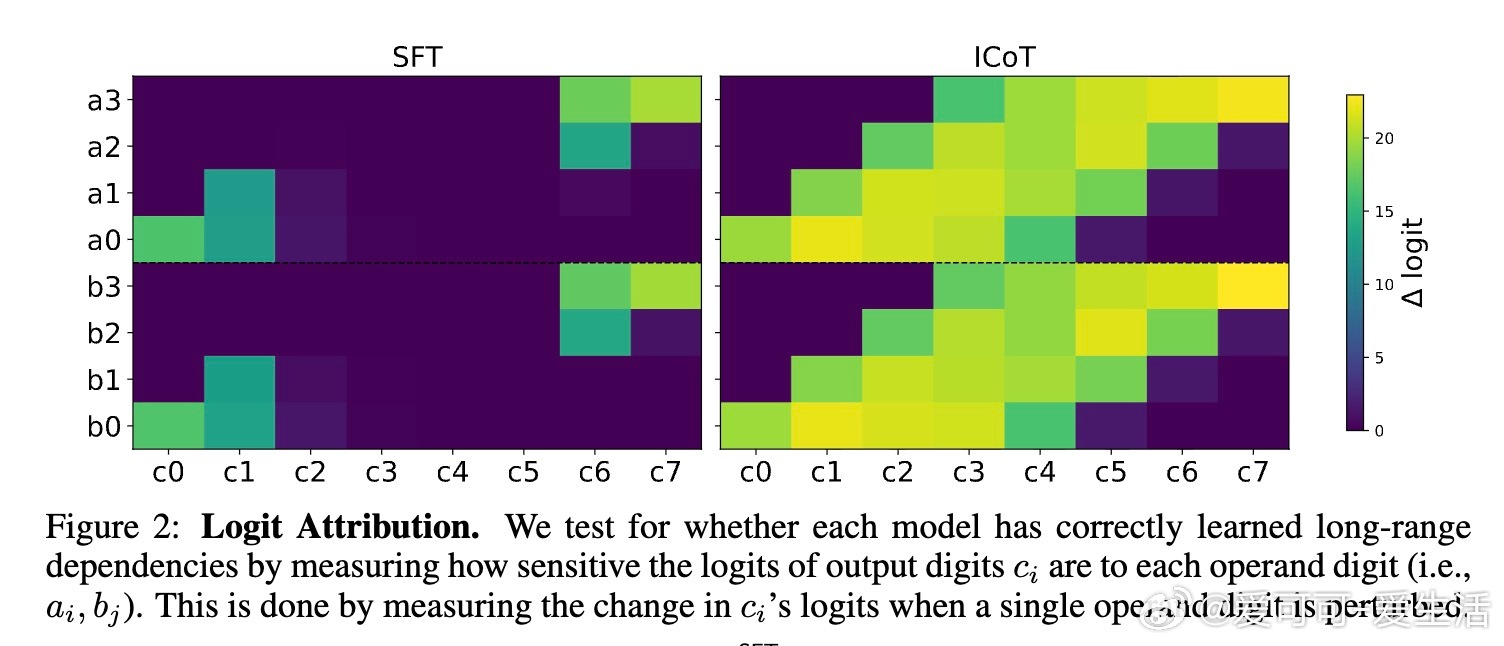
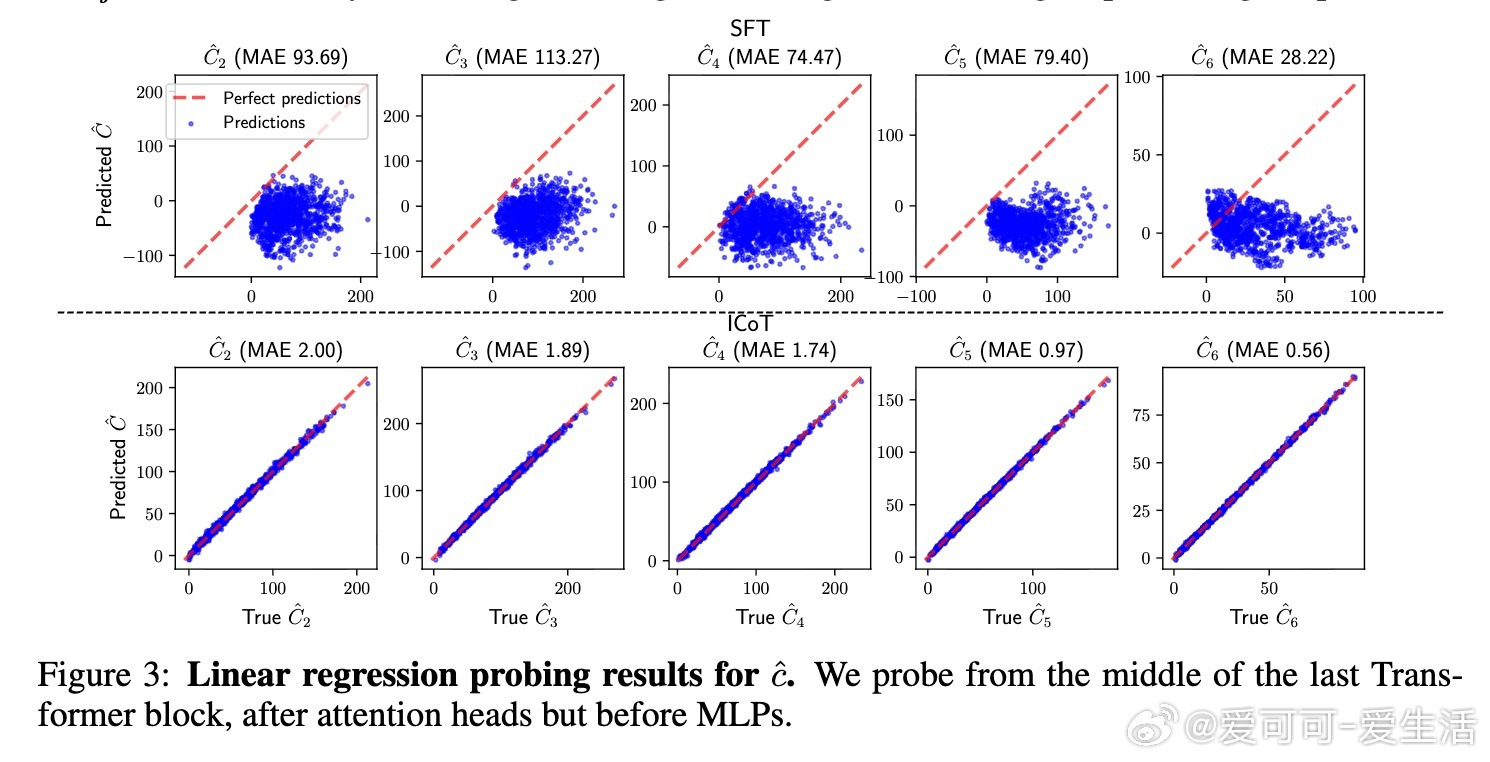
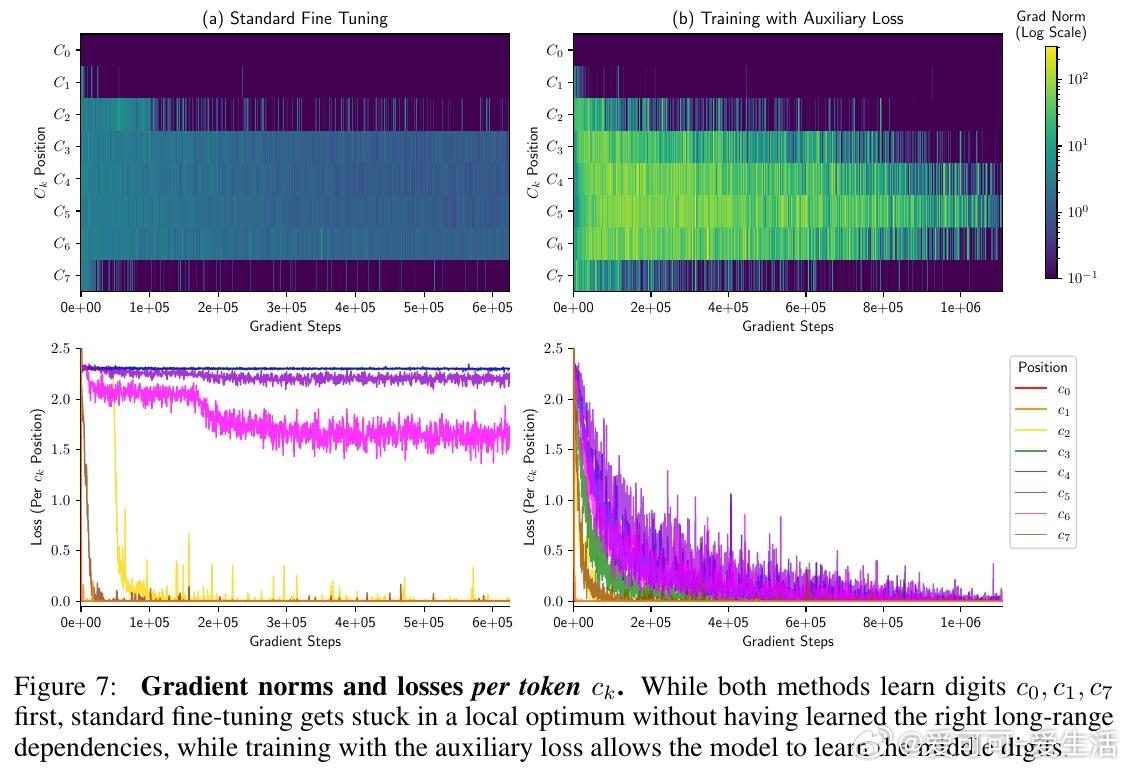
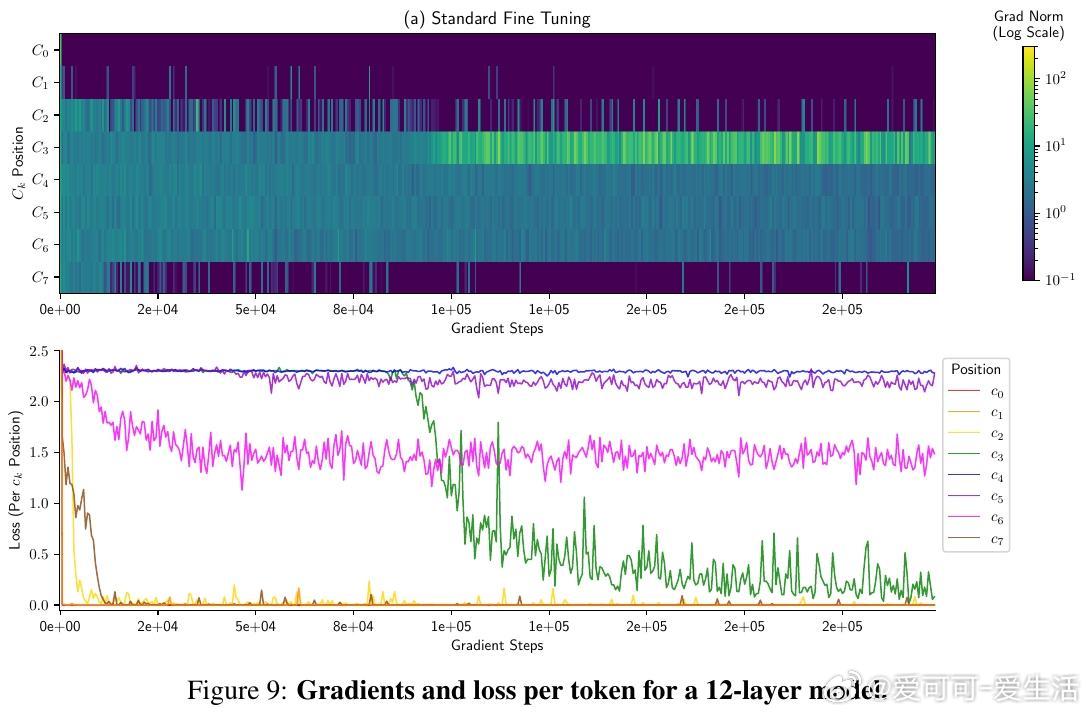
• 标准微调陷入局部最优:传统训练下,模型难以形成上述长程依赖,导致中间乘积位损失停滞,准确率低于1%,且模型扩容无效。
• 简单辅助损失促进突破:引入预测“运行部分和”的线性回归辅助损失,给予模型明确的中间量监督,帮助其学会长程依赖,实现99%以上准确率,无需显式链式思考标记。
• 结果启示:纯梯度下降与自回归损失不易激发Transformer捕捉复杂长程依赖,合理设计任务相关诱导偏置是关键突破口。
心得:
1. 多位数乘法的长程依赖本质,挑战了Transformer的序列建模极限。
2. 任务中间步骤的内隐表示(隐式链式思考)为复杂算法学习提供了可行路径。
3. 利用几何和傅里叶分析揭示模型内部表征,为设计更高效的结构提供理论基础。
详情🔗 arxiv.org/abs/2510.00184
Transformer长程依赖多位数乘法隐式链式思考模型可解释性人工智能