写Python数据处理代码时反复用for循环?这其实是在给程序性能交"税"。NumPy的广播(broadcasting)机制能让你摆脱这种困境——代码量更少,执行更快,关键是思维方式从"逐个迭代"转向"整体形状操作"。掌握这些模式后,你的CPU负载会明显下降。
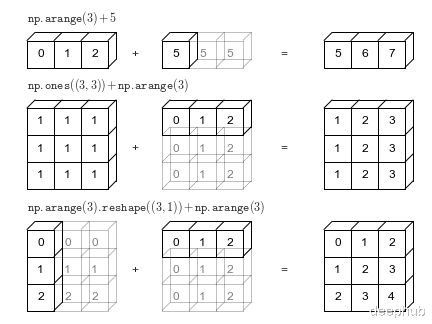
最基础的广播应用。核心思路是让形状自动对齐,而不是手动复制数据。
import numpy as np X = np.arange(12).reshape(3, 4) # (3, 4) row_bias = np.array([1, -1, 0, 2]) # (4,) col_scale = np.array([2, 10, 0.5]) # (3,) X_plus = X + row_bias # (3,4) + (4,) -> row-wise add X_scaled = X * col_scale[:, None] # (3,4) * (3,1) -> col-wise scaleprint("原始矩阵 X:")print(X)print("\n行偏置后 X_plus:")print(X_plus)print("\n列缩放后 X_scaled:")print(X_scaled)
把维度不匹配的轴设为1(用None或np.newaxis),NumPy会在计算时虚拟扩展这些维度,并不真的在内存里复制数据。

跨指定维度广播统计量,完成中心化和标准化。
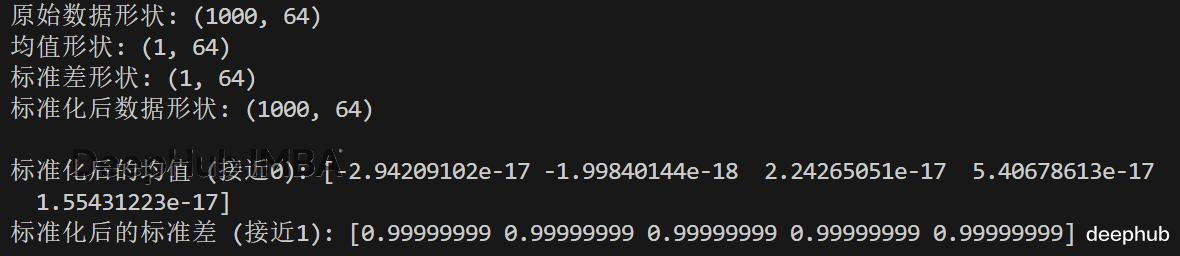
X = np.random.randn(1000, 64) # samples x features mu = X.mean(axis=0, keepdims=True) # (1, 64) sigma = X.std(axis=0, keepdims=True) + 1e-8 Xz = (X - mu) / sigma # (1000, 64) - (1,64)print("原始数据形状:", X.shape)print("均值形状:", mu.shape)print("标准差形状:", sigma.shape)print("标准化后数据形状:", Xz.shape)print("\n标准化后的均值 (接近0):", Xz.mean(axis=0)[:5])print("标准化后的标准差 (接近1):", Xz.std(axis=0)[:5])
这样做的好处显而易见:避免用np.tile做数据复制,数值计算更稳定,代码意图也一目了然。
用[:, None]构造或直接调用np.add.outer系列函数,就能算出所有元素对的组合结果。
a = np.array([1, 2, 3]) # (3,) b = np.array([10, 20, 30, 40]) # (4,) diff = a[:, None] - b[None, :] # (3,4) pairwise differences outer_sum = np.add.outer(a, b) # same idea, explicit APIprint("数组 a:", a)print("数组 b:", b)print("\n成对差值矩阵 (a[:, None] - b[None, :]):")print(diff)print("\n外积和矩阵 (np.add.outer(a, b)):")print(outer_sum)
实际场景里经常需要这种操作:构建价格矩阵、参数网格搜索、距离计算、博弈论收益表等等。

这是广播机制的经典应用案例,计算两个点集中所有点对的距离。
A = np.random.rand(100, 3) # 100 points in 3D B = np.random.rand(200, 3) # 200 points in 3D # (100,1,3) - (1,200,3) -> (100,200,3) then reduce D = np.sqrt(((A[:, None, :] - B[None, :, :]) ** 2).sum(axis=2))print("点集 A 形状:", A.shape)print("点集 B 形状:", B.shape)print("距离矩阵 D 形状:", D.shape)print("\n距离矩阵的前5x5子矩阵:")print(D[:5, :5])print("\n最小距离:", D.min())print("最大距离:", D.max())
数据规模特别大时可以考虑用点积展开的代数形式来优化内存占用,不过对于常见场景,这种广播写法已经够直观也够快了。

批量生成布尔掩码,速度比Python循环快几个数量级。
img = np.random.randint(0, 256, (480, 640, 3)) lower = np.array([20, 0, 0]) # e.g., threshold per channel upper = np.array([200, 255, 80]) mask = (img >= lower) & (img <= upper) # (480,640,3) vs (3,) selected = np.where(mask.all(axis=2)) # pixels within boxprint("图像形状:", img.shape)print("下界阈值:", lower)print("上界阈值:", upper)print("\n掩码形状:", mask.shape)print("符合条件的像素数量:", len(selected[0]))print("符合条件的像素坐标 (前5个):")for i in range(min(5, len(selected[0]))): print(f" ({selected[0][i]}, {selected[1][i]})")
这里的技巧在于,和(3,)向量做比较会自动应用到图像的每个通道上。

卷积本质上就是滑动窗口与卷积核的乘积求和。广播机制能让你快速验证算法逻辑。
from numpy.lib.stride_tricks import sliding_window_view x = np.arange(20) # (20,) win = sliding_window_view(x, 5) # (16, 5) kernel = np.array([1, 0, -1, 0, 1]) # (5,) y = (win * kernel).sum(axis=1) # (16,) -> fast 1D conv-like op#注意sliding_window_view 是 NumPy 1.20.0+ 才添加的功能,如果我写了个自定义函数,可以直接用def sliding_window_view(x, window_size): from numpy.lib.stride_tricks import as_strided """创建滑动窗口视图(兼容旧版本NumPy)""" shape = (x.shape[0] - window_size + 1, window_size) strides = (x.strides[0], x.strides[0]) return as_strided(x, shape=shape, strides=strides)print("输入信号 x:", x)print("\n滑动窗口形状:", win.shape)print("卷积核:", kernel)print("\n卷积结果 y:", y)print("结果形状:", y.shape)
代码可读性很高,同时避免了在窗口上做Python循环的性能损失。

按组计算统计量,然后广播回原始数据——不需要循环,也不用做表连接。
values = np.array([5, 6, 7, 3, 2, 9, 8]) groups = np.array([0, 0, 0, 1, 1, 2, 2]) # group id per row # group means via bincount sums = np.bincount(groups, weights=values, minlength=groups.max()+1) counts = np.bincount(groups, minlength=groups.max()+1) means = sums / counts # (num_groups,) centered = values - means[groups] # broadcast per rowprint("原始值:", values)print("分组 ID:", groups)print("\n各组求和:", sums)print("各组计数:", counts)print("各组均值:", means)print("\n中心化后的值:", centered)
这种模式在特征工程里很常见,比如要按商店、用户群或时间段来做归一化。

把日度数据和对应的周期性基线做比较,是时间序列分析的常规操作。
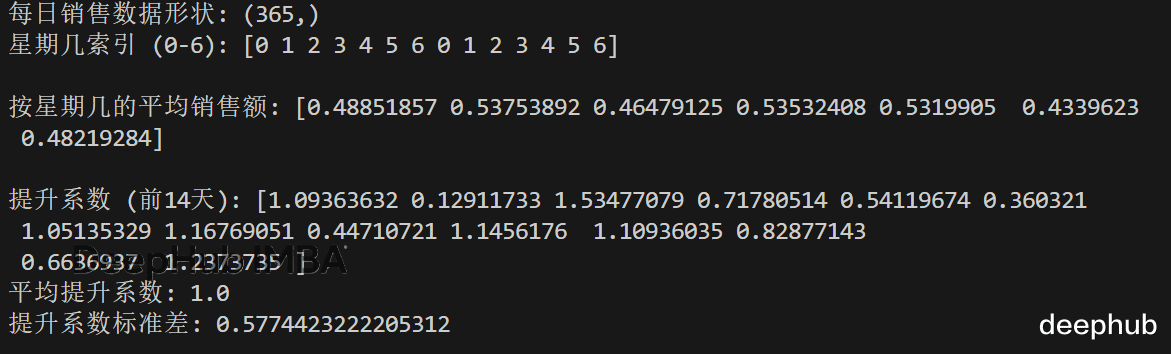
daily = np.random.rand(365) # sales per day dow = np.arange(365) % 7 # day-of-week index 0..6 avg_by_dow = np.bincount(dow, weights=daily, minlength=7) / np.bincount(dow, minlength=7) lift = daily / avg_by_dow[dow] # broadcast (365,) vs (7,)print("每日销售数据形状:", daily.shape)print("星期几索引 (0-6):", dow[:14])print("\n按星期几的平均销售额:", avg_by_dow)print("\n提升系数 (前14天):", lift[:14])print("平均提升系数:", lift.mean())print("提升系数标准差:", lift.std())
几行代码就能算出每天相对于同星期平均值的"提升系数",不用写任何显式循环。
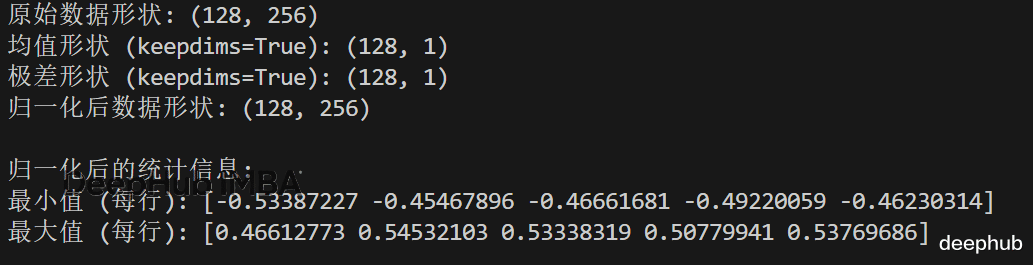
保持维度能让后续运算自然对齐,省去很多reshape操作。
X = np.random.randn(128, 256) mu = X.mean(axis=1, keepdims=True) # (128,1) rng = X.ptp(axis=1, keepdims=True) # (max-min) X01 = (X - mu) / (rng + 1e-8) # works without reshapingprint("原始数据形状:", X.shape)print("均值形状 (keepdims=True):", mu.shape)print("极差形状 (keepdims=True):", rng.shape)print("归一化后数据形状:", X01.shape)print("\n归一化后的统计信息:")print("最小值 (每行):", X01.min(axis=1)[:5])print("最大值 (每行):", X01.max(axis=1)[:5])
经验法则:如果计算出来的统计量后面还要参与减法或除法,那就用keepdims=True,能避免形状调整的麻烦。
同时在多个轴上做广播——这类场景下循环代码基本可以彻底退场了。
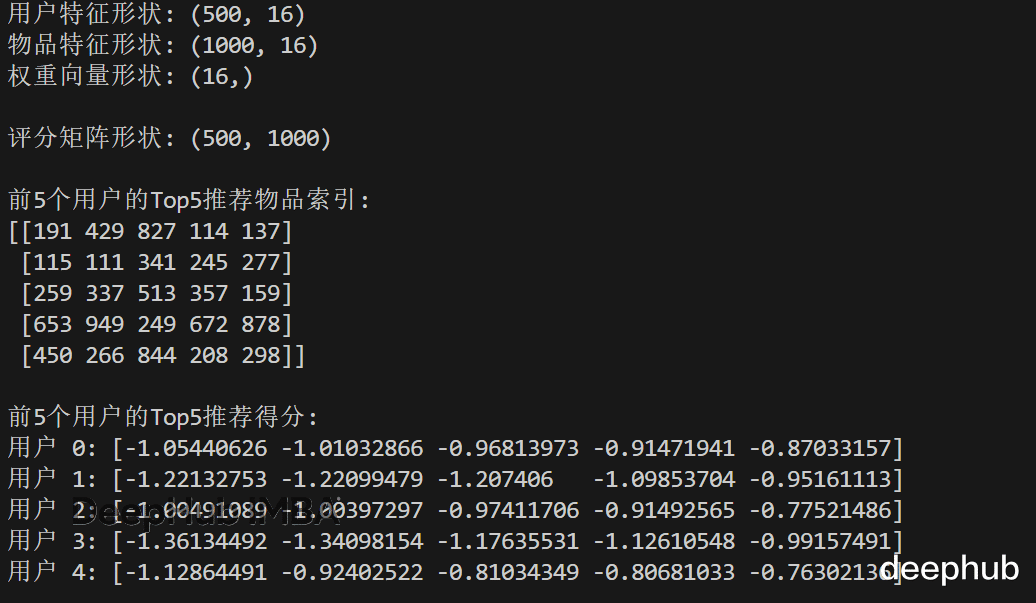
# Score every user against every item with per-dimension weights users = np.random.rand(500, 16) # (U, D) items = np.random.rand(1000, 16) # (I, D) w = np.linspace(0.5, 2.0, 16) # (D,) # (U,1,D) * (1,I,D) * (D,) -> (U,I,D) then reduce scores = (users[:, None, :] - items[None, :, :])**2 * w scores = -scores.sum(axis=2) # higher is better top5 = scores.argsort(axis=1)[:, -5:]print("用户特征形状:", users.shape)print("物品特征形状:", items.shape)print("权重向量形状:", w.shape)print("\n评分矩阵形状:", scores.shape)print("\n前5个用户的Top5推荐物品索引:")print(top5[:5])print("\n前5个用户的Top5推荐得分:")for i in range(5): print(f"用户 {i}: {scores[i, top5[i]]}")
推荐系统、排序算法这类需要大规模打分的场景,用广播能把核心逻辑压缩到几行代码里。
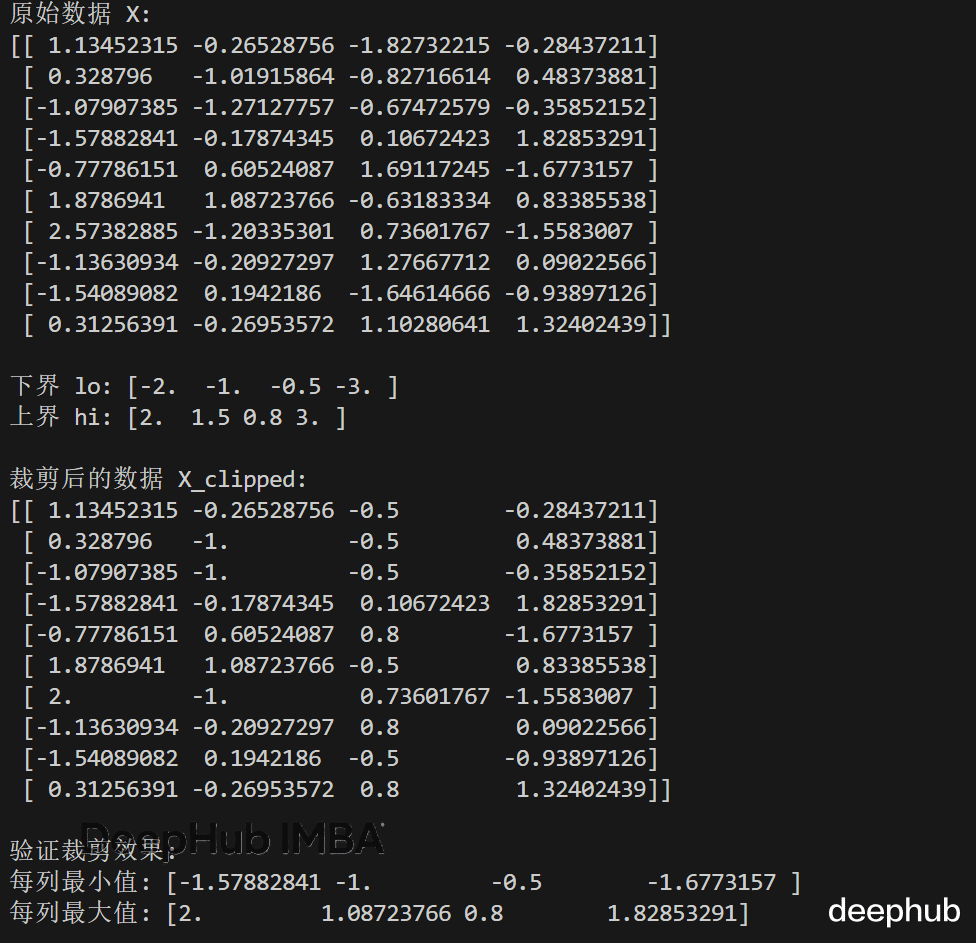
对不同特征使用不同的上下限,不需要拆分数组。
X = np.random.randn(10, 4) lo = np.array([-2.0, -1.0, -0.5, -3.0]) hi = np.array([ 2.0, 1.5, 0.8, 3.0]) X_clipped = np.minimum(np.maximum(X, lo), hi) # (10,4) vs (4,)print("原始数据 X:")print(X)print("\n下界 lo:", lo)print("上界 hi:", hi)print("\n裁剪后的数据 X_clipped:")print(X_clipped)print("\n验证裁剪效果:")print("每列最小值:", X_clipped.min(axis=0))print("每列最大值:", X_clipped.max(axis=0))
如果需要对数组不同边做不对称填充,可以构建(N, 2)形状的左右填充量数组,再广播到目标形状——通常比写条件分支代码简单。
用C语言级别的速度生成one-hot或multi-hot编码。
labels = np.array([2, 0, 1, 2, 2, 3]) # ids num_classes = labels.max() + 1 one_hot = (labels[:, None] == np.arange(num_classes)[None, :]).astype(np.uint8) print("原始标签:", labels)print("类别数量:", num_classes)print("\nOne-hot编码矩阵:")print(one_hot)print("\n编码矩阵形状:", one_hot.shape)print("\n验证: 每行之和应该为1")print("每行之和:", one_hot.sum(axis=1))
处理多标签分类时,可以对(n_samples, n_labels)形状的标签集做广播,再用.any(axis=1)做归约。

判断两个数组能否广播其实有简单规则:
从右向左对比形状(trailing axes),如果对应位置的维度相等或者有一个是1,就能广播。需要的话就用None插入长度为1的轴来强制对齐。
理解这个规则后,你会发现很多地方的循环代码其实都可以用广播改写。
广播会创建很大的虚拟形状,要靠归约操作来控制实际内存用量。如果(U,I,D)这种三维张量撑爆内存,就对U或I分块处理。
能用keepdims就用,后续操作会轻松很多。
类型转换要克制。最好在数据流的边界做一次类型转换,核心计算部分保持稳定的dtype。
代码注释里标注形状很有帮助,比如# (U,1,D)这种小提示,回看代码时会感谢当时的自己。
总结广播是NumPy里最让人恍然大悟的特性。掌握后能去掉大量循环,让代码意图更清晰,同时获得向量化带来的性能提升——而且不需要引入什么复杂工具。
从形状对齐入手,合理使用keepdims,在维度不匹配时灵活运用None。练多了代码里的for循环自然就少了。
https://avoid.overfit.cn/post/9c593c1cebc54c2fabd9ea0c3f1cbfcb