本期给大家分享2025武汉高三九月调考的数学试卷，基础和中档题约 105 分，难题约 45 分。难题分布在第 7、8、11、14、18 (2) 和 19 (2)(3) 题， 18 题解析几何和 19 题导数压轴题。

选择题考点几乎涵盖高中数学核心领域，第一部分 8 道题依次涉及集合运算（解一元二次不等式后求交集）、复数四则运算（根据等式求复数）、双曲线的渐近线性质（由渐近线方程求参数比值的绝对值）、等比数列求和（正方形面积递推形成等比数列，求前 n 项和）、奇函数的性质（利用奇函数定义求参数）、排列组合（不同元素分配问题）、三角形中的三角函数关系（利用内角和与三角公式求正切值）、椭圆的离心率（结合垂直关系与线段比例求离心率）；第二部分 3 道题则分别考查三角函数的图象与性质（周期、相位、对称点、图象变换后的单调性）、基本不等式的应用（由正实数和的条件判断各项取值范围）、随机事件的概率（独立性、概率运算、概率大小比较），整体覆盖代数、几何、概率统计三大模块。

3 道填空题分别对应不同核心知识模块，考点分布清晰且具有代表性。第 12 题考查平面向量的模长计算，需利用向量模长公式与数量积的关系；第 13 题考查等差数列与等比数列的综合应用，通过 “等差数列中三项成等比数列” 的条件，结合等差数列通项公式与等比数列性质建立方程，求解参数比值的绝对值，体现两类数列知识的交叉融合；第 14 题考查立体几何中的线段长度求解，依托四棱锥模型，结合线面垂直性质与菱形的几何特征，需通过空间几何关系分析与计算得出PA的长度，覆盖立体几何的核心考点。

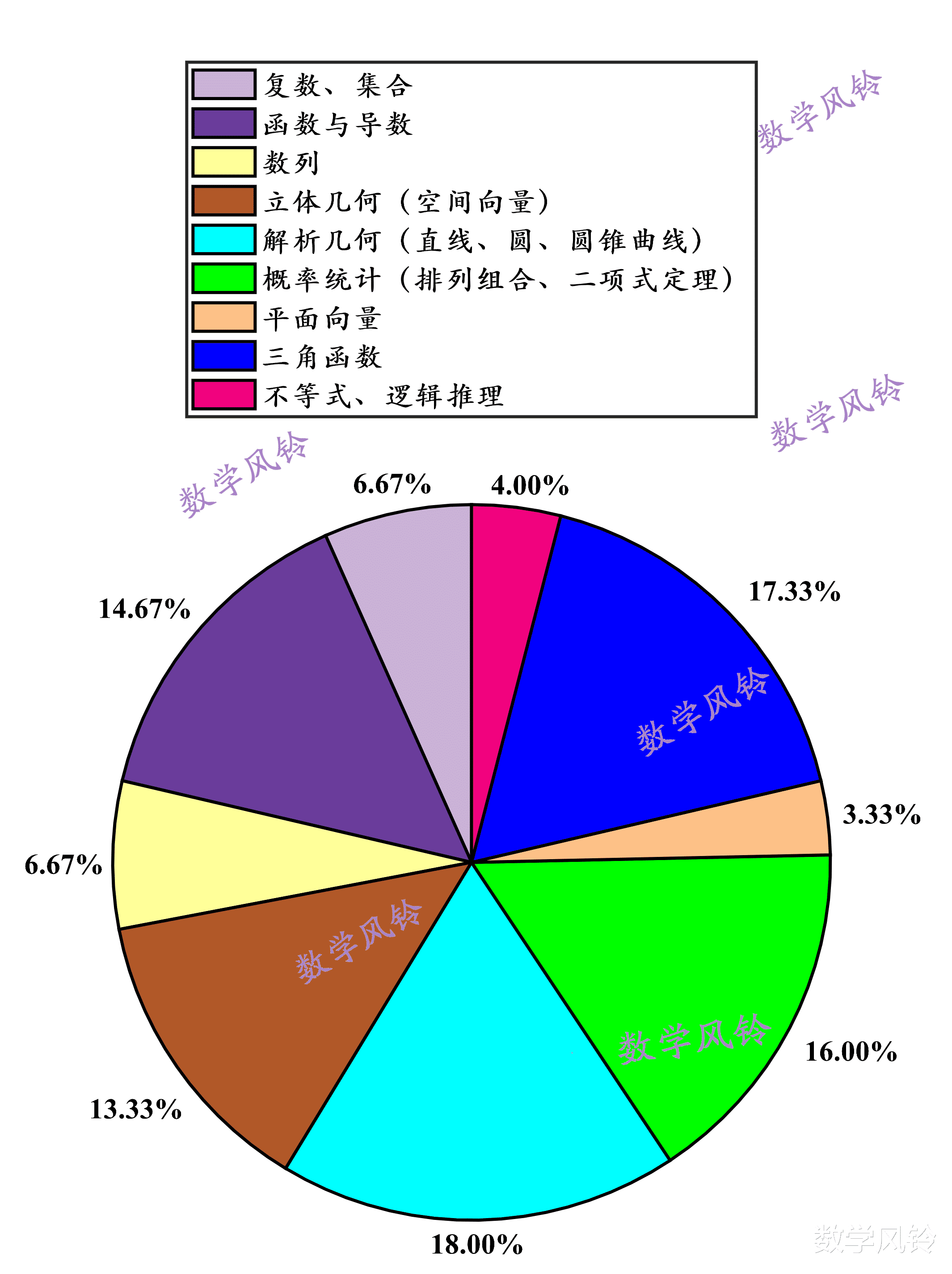
本套试卷不同知识点的分值占比如下图所示：